I alla rörelser förekommer en viss energi. Då energi aldrig bokstavligt försvinner förs det dock över till andra ställen. Om man till exempel puttar på ett objekt så tillför man visserligen kraft, men man kan säga att denna kraft har åstadkommits tack vare (kemisk) energi som redan fanns i din kropp.
På samma sätt, då ett objekt bromsas av friktion försvinner inte denna energi, utan den omvandlas till termisk energi, med andra ord, värme. Då det finns så många typer av energi har man valt att dela in de I två övergripande kategorier: Kinetisk energi, och potentiell energi.
Kinetisk Energi
Kinetisk energi (även kallad rörelse energi) definieras som det mekaniska arbete som skulle krävas för att få en kropp att försättas i rörelsen den befinner sig i. Alltså beror den på hur snabbt denna kropp rör sig.
Formeln för en kropps kinetiska energi ser ut som så
Som ni kan se är det oviktigt i vilken riktning objektet färdas. Kinetiska energin beror endast på farten (hastighetsvektorns längd).
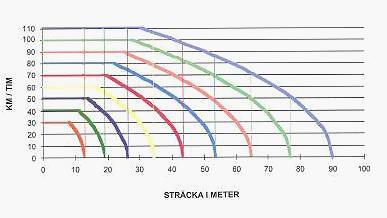
Kinetisk energi visar oss dessutom hur svårt det är att bromsa objekt. Ett kul exempel som man lär sig på trafikskolan är att när man dubblar sin fart så dubblar man inte bara sin bromssträcka, utan man kvadrupplera den!
Titta noga på formeln: Ni ser väl att farten är kvadrerad? Det gäller nämligen att om farten ökar med en konstant så ökar kinetiska energin med .
Effekt och Kinetisk energi är båda väldigt tätt relatarede. Låt oss härlde detta.
Effektlagen
Effekt och Kinetisk energi är båda väldigt tätt relaterade. Som ni kanske redan vet gäller det att . Om vi nu tittar på rörelse energins formel, så kan ni se att:
Om vi nu tidsderiverar detta får vi:
Eftersom vi vet att så kan vi skriva att
Vi vet dock att formeln för en krafts effekt är
Alltså har vi att . Detta är den så kallade Effektlagen.
Arbetslagen
Vi vet att . Om vi använder effektlagen kan vi skriva om detta till:
Om man integrerar detta får vi helt enkelt
Detta är Arbetslagen! Ändringen av den kinetiska energin under en tid är alltså lika med ett arbete under samma tid.