Potentiell Energi
En kropps potentiella energi är en sorts lagrad energi, som förekommer oftast i samband med så kallade konservativa krafter.
Konservativa krafter förändras inte utav vägen som angreppspunkten tar utan endast av dess start och slutläge i rörelsen. Exempel på dessa är fjäderkraften, tyngdkraften, gravitationskraften etc.
Potentiella energins formel är:
Potentiella energin mäts i ett visst läge. För att beräkna den måste man välja en referenspunkt , som kan vara godtycklig. För att förklara hur det här fungerar kan vi ta några exempel.
För fjäderkraften
Ta till exempel en fjäder vars fjäderkomstant är och vars jämviktsläge är i . Vi trycker på den med en kraft så att den hamnar i läget .
Enligt Hookes lag måste alltså kraften vara så stark som .
Vad är då fjäderns potentiella energi när den är intryckt?
Kraftens angreppspunkt har nu rört sig enbart horisontellt från läget till läget . Dessutom har :s riktning och styrka varit konstanta under rörelsen. Fjäder kraften kommer att vara lika stark som kraften fast mottriktad.
Om vi då applicerar formeln vi precis lärde oss får vi alltså:
Vilket till slut blir:
För tyngdkraften
I detta exempel har vi att ett föremål som rör sig från punkt till , vars höjdskillnad är
(så att ).
I detta fall blir då formeln:
Energiprincipen
Mekanisk energi är helt enkelt summan av den potentiella och kinetiska energin:
När ingen friktion förekommer så bevaras den mekaniska energin! Alltså varierar potentiella och kinetiska energin, men deras summa är konstant - de "förs över" till varann:
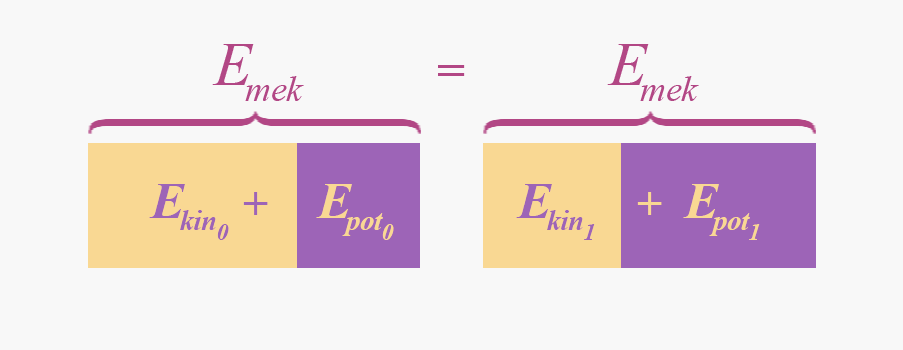
Tack vare detta kan vi alltså dra en hel del nytta av dessa saker i problem där friktion försummas eller inte finns, vilket gör de väldigt användbara.