Kraft Effekt
En krafts effekt betecknas ofta som (som i 'Power'). Man skulle kunna få en liten hint om vad detta begrepp betyder av dess svenska namn. En Krafts Effekt är nämligen en krafts inflytande på en rörelse. Den beräknas med formeln , där är kraften i fråga, och är hastighetsvektorn till rörelsen.
Om är negativ, betyder det att motverkar rörelsen. Om är positiv så medverkar rörelsen.
Det är ganska intressant att veta hur man åstadkommer denna tolkning utifrån denna beräkning. Titta på skalärprodukten som utförs:
Från linjär algebra kanske ni kommer ihåg att en formel för skalärprodukten var:
Där är vinkeln mellan båda vektorerna.
Varför är detta så intressant? Jo som ni vet så är cosinus av en vinkel positiv då vinkeln är mindre än 90°, och negativ när den är större.
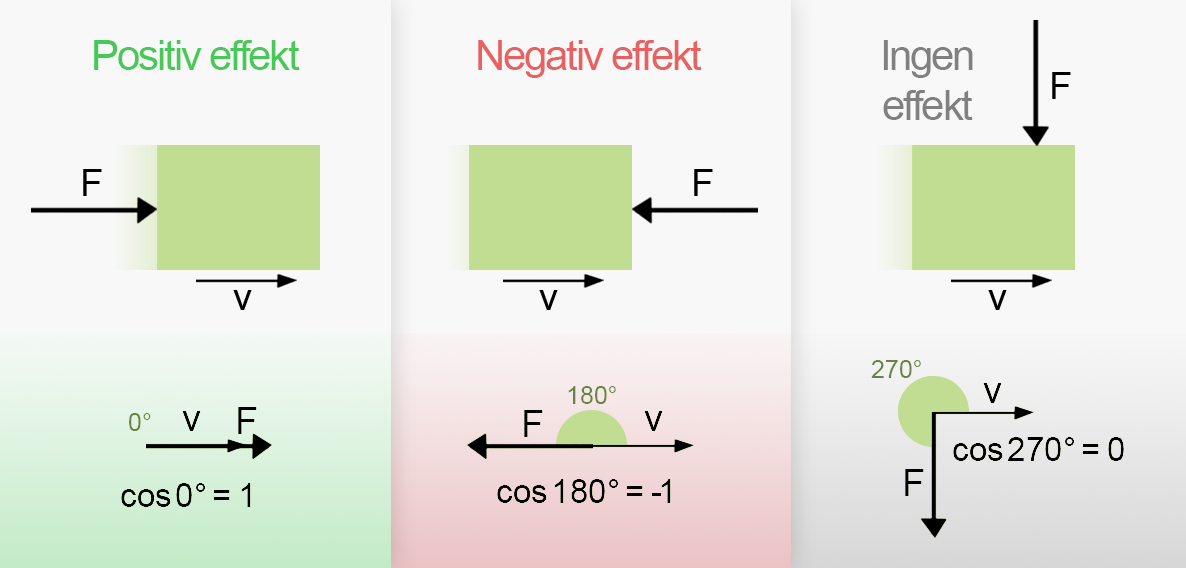
Visst blir det galet enkelt så fort man ritar upp det!? Om kraften är mottriktad hastigheten så är det väl klart att den motverkar den, och motsatsen är även sann. Samtidigt har vi att då en kraft är vinkelrät mot rörelsen så har den INGEN effekt på hastigheten, eller i varje fall inte dess horisontella komponent . Kraften kommer nämligen att accelerera objektet vertikalt. Men är då oförändrad.