Vad är en riktningsderivata och hur hittar man den?
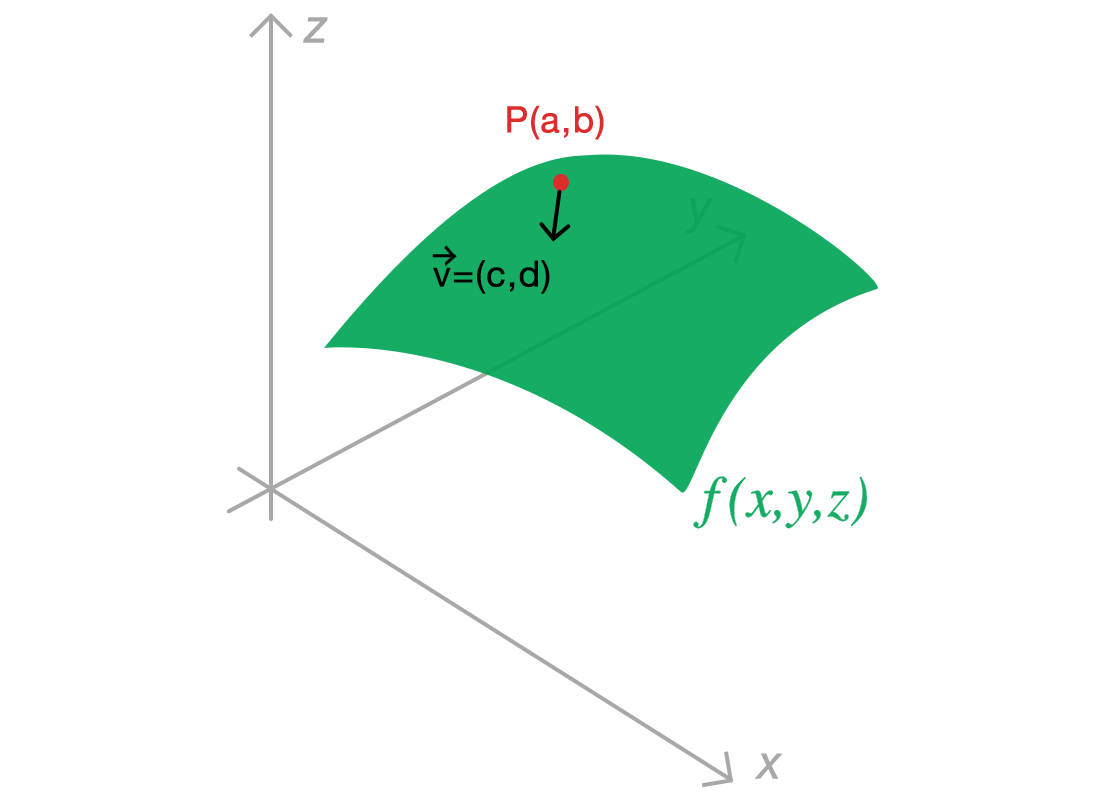
Låt säga att vi har en funktion som vi ritar upp i planet (se den gröna kroppen på bilden nedanför). Vi har sedan en punkt på den här kroppen samt en riktning .
Vi vill nu veta hur stark lutningen är på ytan om man står på punkten P och går i riktningen .
Vi vill alltså räkna ut riktningsderivatan för funktionen i punkten och riktningen .
Riktningsderivatan betecknas (eller ) och räknas ut med formeln:
Om ni kommer ihåg gradientens definition förstår ni också varför formeln kan förenklas till det här:
(observera att punkten mellan vektorerna antyder att det rör sig om en skalärprodukt)
OBS! Innan man applicerar formeln för riktningsderivatan måste man se till att vektorn är normerad, d.v.s. att den har längden 1!
Uppgift 1
Beräkna riktningsderivatan av funktionen från punkten till punkten
Lösning
Vi räknar först ut riktningsvektorn
Vi kollar nu vad vektorn har för längd:
Eftersom vi vill att riktningsvektorn ska vara normerad, måste vi alltså dela den på . Vi får då:
Nästa steg är att räkna ut funktionens partiella derivator:
Vi sätter nu in punkten (1,1) i våra partiella derivator och får:
Slutligen applicerar vi formeln för riktningsderivatan:
Riktningsderivatan är alltså
Största och minsta värde
Som vi såg innan kan formeln för riktningsderivatan skrivas: .
Kommer ni ihåg skalärproduktens definition från Linjär Algebra? Den säger att
Detta betyder alltså att riktningsderivatans formel kan skrivas som:
vilket i sin tur kan förenklas till:
eftersom v är en enhetsvektor!
Som alltid gäller:
Alltså har vi också:
Med denna härledning har vi kommit fram till riktningsderivatans största och minsta värden!
Definition:
Riktningsderivatans minsta värde antas då pekar i riktningen:
Riktningsderivatans största värde antas då pekar i riktningen:
Exempel:
Låt . I vilken riktning växer som snabbast från punkten ?
Svar:
Vi söker riktningsderivatans största värde. Enligt definitionen ovan ska detta vara detsamma som att räkna ut gradienten till f!
Vi får:
Vi sätter in punkten (1,2) i gradienten:
Funktionen växer alltså som snabbast i riktningen (2,4), vilket kan förenklas till (1,2)!
Man kan även ta det här ett steg längre och normera riktningen vi fick fram. Isåfall får vi: