Beteckning:
Normalfördelningen förekommer i vanligt tal i två former:
Allmänna normalfördelning
Standardiserad normalfördelning
Den standardiserade versionen är en förenkling av den allmänna. Båda kommer till stor användning inom sannolikhetsteorin som vi snart kommer att upptäcka. I allmänhet är normalfördelningen utan tvekan den viktigaste sannolikhetsfördelningen i hela sannolikhetsteorin.
Den normalfördelningen beror på två parametrar, och som representerar fördelningens väntevärde respektive standardavvikning. Detta ger att om är en normalfördelad S.V gäller följande:
Den standardiserade versionen har bestämda värden för dessa parametrar, och . Detta gör att den standardiserade normalfördelningens beteckning blir .
Den standardiserade normalfördelningen
Beteckning:
Formeln för den standardiserade normalfördelningen ges av täthets- och fördelningsfunktionen:
Notera ovan att den standardiserade normalfördelningens täthets- och fördelningsfunktion har egna beteckningar, respektive som används flitigt då den standardiserade versionen är ytterst viktigt trots förenklingen.
Som tidigare nämnt är och normalfördelningens väntevärde respektive standardavvikning vilket ger att den standardiserade normalfördelningens vändevärde och standardavvikning .
Kvantiler
Tack vare den standardiserade normalfördelningens användbarhet har även kvantilbeteckningar med förberäknade värden införts för att underlätta beräkningar.
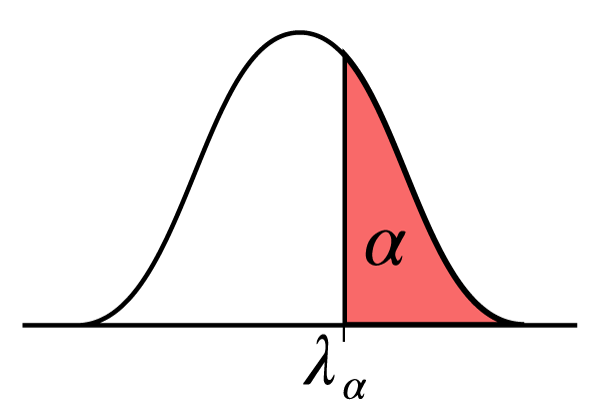
Kvantiler kan förklaras som ett värde på den standardiserade normalfördelningens x-axeln där arean till höger om detta värde är och motsvarar -kvantilen så att .
Allmänna normalfördelningen
Beteckning:
Formeln för den allmänna normalfördelningen kan enklast uttryckas med hjälp av den standardiserade normalfördelningens täthets- och fördelningsfunktion med en minmal förändring. Denna förändring gör den allmänna formen beroende av och .
Detta utvecklas sedan till den fullständiga formeln för den allmänna normalfördelningen:
Som tidigare nämnt motsvarar väntevärdet och standardavvikelsen. För att förtydliga hur normalfördelningen beror av parametrarna kan vi ta en titt på illustrationen nedan. Den vänstra bilden visar två normalfördelningar med samma väntevärde men olika standardavvikelser. Det rödmarkaderade fördelningen har en lägre standardavvikelse, ett lägre värde på än den mera tillplattade fördelningen . Detta gör att den rödmarkerade fördelningen blir spetsigare och mindre utspridd.
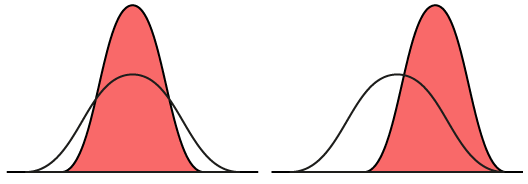
I den högra grafen ser vi två fördelningar som dessutom skiljer i väntevärde . Den rödmarkerade fördelningen som har ett högre väntevärde än den tillplattade blir därmed förskjuten i x-led till det område det tilldelade väntevärdet finns.
Centrala gränsvärdessatsen
Detta område är bland det viktigaste i hela sannolikhetskursen. Det kommer på alla tentor och flera gånger på olika uppgifter ibland.
Centrala gränsvärdessatsen är en väldigt förbryllande sats som säger att om vi har ett tillräckligt högt antal oberoende S.V med samma fördelning kan summan av dessa variabler approximeras till en normalfördelning.
Mera formellt uttryckt: Om vi har en följ S.V. som är likafördelade och oberoende och gäller approximativt .
Exercise
På en godiskiosk anländer sötsugna studenter för at köpa karameller. Antag att tiden mellan ankomster är oberoende, likafördelade s.v. med väntevärdet minuter och standardavvilkelsen minuter.
Beräkna antalet studenter som anländer från till så att sannolikheten att det kommer studenter eller fler under den angivna tidsperioden är . Nedan återfinns även en tabell som kan komma till användning.
0.15 0.10 0.05 0.025 1.0365 1.2816 1.6449 1.960
Solution
Vi vill mäta tiden mellan ankomsterna för antalet sötsugna studenter . Detta innebär detta att de S.V. som mäter tiden mellan ankomsterna är . Den angivna tidsperioden är timmar som motsvarar minuter och väljer att räkna i minuter så att varje S.V. motsvarar tiden i minuter mellan varje ankomst.
Istället för att räkna på antal olika S.V räknar vi numera på den totala tid som det tar för studenter att anlända. Sannolikheten för att det kommer personer eller fler ges av tidsjämförelsen .
Sannolikheten att det kommer studenter eller fler är ekvivalent med sannolikheten att den totala tiden för studenternas ankomst understiger eller motsvarar minuter. Detta ger oss att
Vi antar nu att är approximativt normalfördelad så att
Detta ger oss att
och avslutningen ekvationen
Vi löser ut och får svaret personer.