Lite övande!
För att låta det här sjunka in provar vi med några enkla fall. Vi använder samma låda, fast med kraften på dessa ställen:
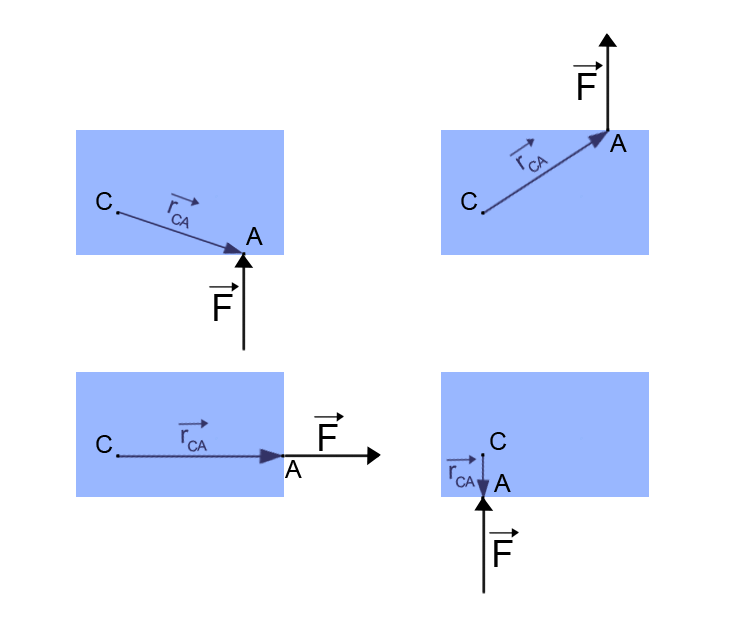
Men först måste vi som i många andra mekanik problem sätta ut ett koordinatsystem.
Låt oss sätta dessa så att .
Exempel 1) - som förr
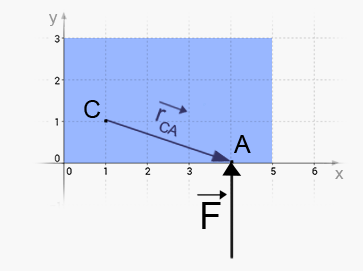
I detta fall har vi att , , , .
Eftersom detta är precis det exemplet vi höll på med förut så kan vi direkt säga att
Så stark är alltså vridningen. Men vad är då "kortaste" vinkeln som dessa två vektorer bildar? Vi behöver inte nödvändigtvis beräkna detta, vi behöver bara ungefärligen hur denna vinkel ser ut. För detta kommer att ge oss vridningens riktning. Den följer nämligen skruvens riktning (cf Algebra kryssprodukt). I detta fall får vi att vridningen är positiv, alltså moturs. Precis som vi såg förut!
Exempel 2) - Längs samma verkningslinje
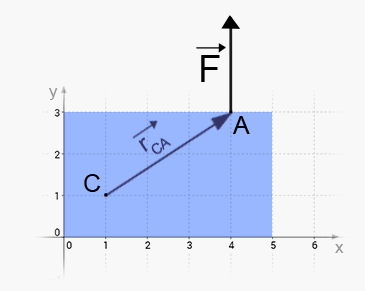
Nu verkar kraften F på angreppspunkten i stället (Det är fortfarande samma kraft, alltså har den samma riktning). Nu får vi alltså samt
Som ni kan se har den "kortaste vinkeln" fortfarande en positiv riktning. Alltså är denna vridning också moturs.
Men...nu blev kraften bara densamma...varför det? Jo ni kanske lade märke till att vi flyttade upp angreppspunkten längs samma linje som F gick i 1). Detta råkar vara F:s verkningslinje, men mer om det sen.
Nu kommer lite tuffare piller att svälja, så vi byter låda en stund.
Exempel a)
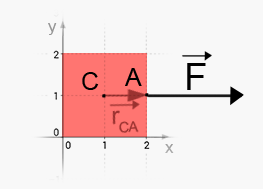
Det kan verka rätt självklart att den här lådan inte kommer rotera. I första hand kan man snabbt konstatera att är parallell med vilket gör att deras kryssprodukt (med andra ord vridningsmomentet) måste vara . I andra hand kan man säga att denna kraft inte kan orsaka någon vridning, eftersom kraftens verkningslinje går genom lådans masscentrum (i detta fall C). Detta är ju fallet.
Exempel b)
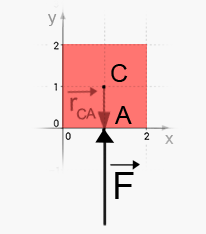
??ven i detta exempel konstaterar vi att även om kraften nu puttar på lådan i stället för att dra den, så orsakas ingen vridning av lådan. Detta av samma anledningar som i a), vektorerna må vara motriktade, men de är ändå parallella.
Exempel c)
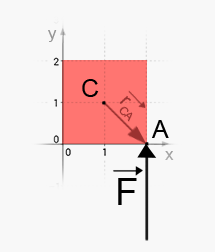
Nu kommer nog säkerligen lådan att rotera som så:
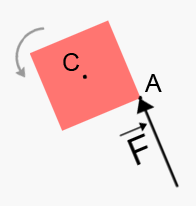
Vi kan till och med räkna ut det:
Vridningskraften är alltså och dess riktning är positiv (moturs).
Exempel 3) - Parallella vektorer
Vi tar nu en ny horisontell kraft F så att på angreppspunkten
A=(5,1,0)A=(5,1,0) . Detta gör att , vilket gör till att är parallell med
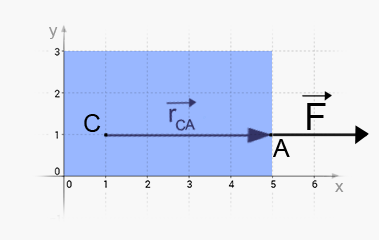
Det finns två saker man kan komma att tänka på när den här kraften verkar på just denna låda. En av de är att den här kraften kommer få lådan att vrida sig, i med att den inte drar längs dess horisontella mitt-axel.
Men om man snabbt räknar så tänker man på en annan sak... vridningsmomentet i C blir ju ! Se här:
Detta gäller även fast man intuitivt kan konstatera att lådan kommer vridas. Det beror på att man oftast (och i detta fall) beräknar vridningsmomentet med avseende på en punkt, och inte ett helt objekt, som en låda. Lådan roterar, men inte just punkten C. Andra punkter på lådan, som till exempel lådans masscentrum (inte C i detta fall), kommer att vridas.
Exempel 4) - Motsatta vektorer
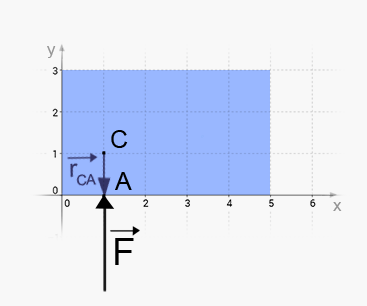
Nu verkar kraften på angreppspunkten . Vi får då , samt att .
Alltså är vridningen i C ännu en gång .