Efter smällen
I förra avsnittet tittade vi på ögonblicket då en stöt sker. Vi ska nu kolla på vad som händer efter den. Hur två objekt reagerar efter att ha stött i varandra beror på bland annat deras hastighet, vikt, och elasticitet.
En otroligt bra föreläsning som förklarar dessa hittar ni här:
Jag rekommenderar starkt att ni kollar på hela videon, mycket som kan verka luddigt och oklart blir väldigt tydligt när Walter Lewin förklarar det.
Men för att sammanfatta:
Hur föremål beter sig efter kollisioner beror bland annat på deras elasticitet. En kollisions elasticitet mäts tack vare stöttalet:
De värden ni mest realistiskt kommer stöta på (no pun intended...) är:
, en fullständigt elastisk kollision, med andra ord objektens separationshastigheten är lika med deras kollisionshastighet.
, en fullständigt oelastisk kollision, med andra ord objektens separationshastighet är 0. Tänk till exempel en lerboll mot en vägg. Efter kollision fastnar lerbollen i väggen, och väggen rör sig inte heller.
Om vi ser på det här exemplet:
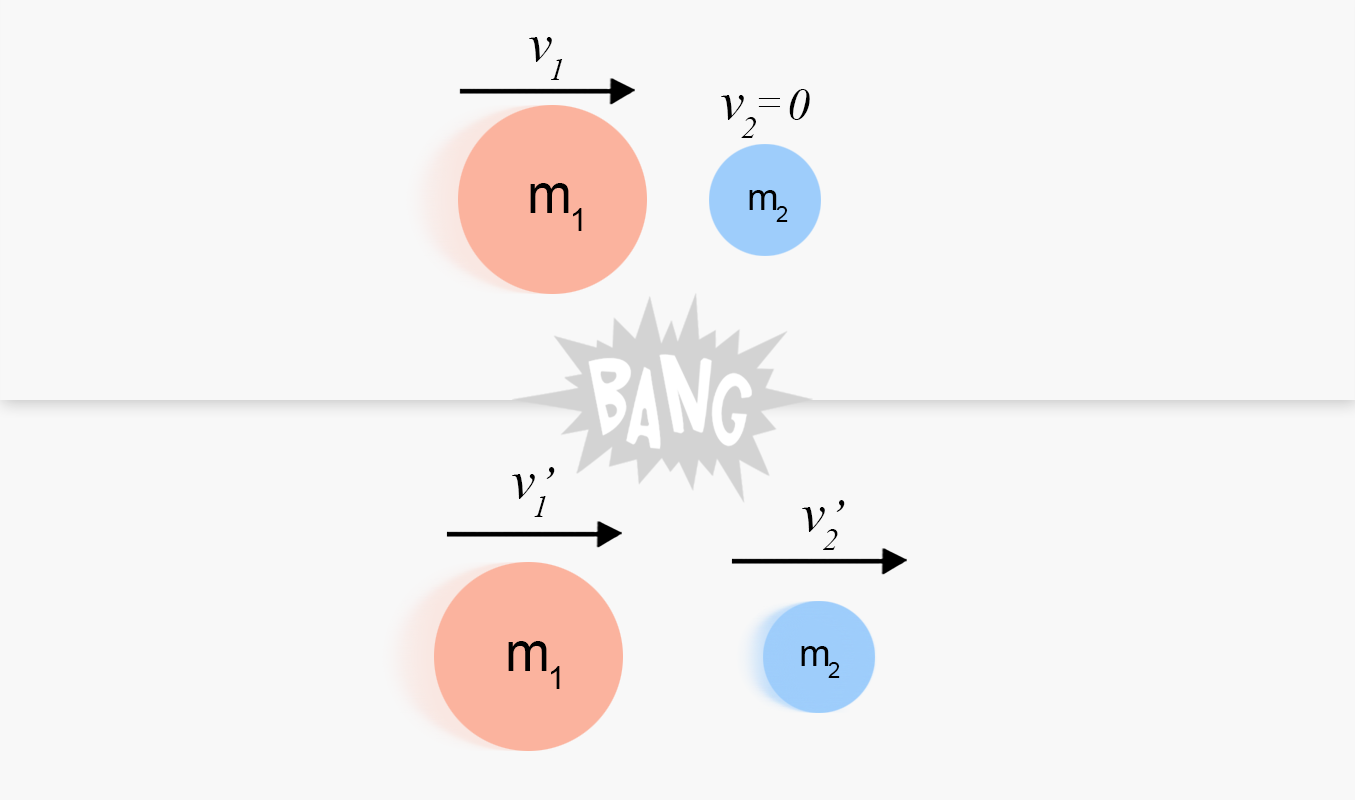
I detta fall har vi att den så kallade relativa separationshastigheten är:
och den relativa kollisionshastigheten är:
Alltså har vi att:
Detta stöttal är en så kallad materialkonstant, med andra ord, ett par av objekt kommer alltid att ha samma stöttal! Alltså om man kan vi använda oss av stöttalet för att beräkna objektens fart före eller efter kollision, beroende på vilka värden vi redan känner till. Detta bland annat tack vare det vi härledde i förra avsnittet.
stötlagen:
Vilket vi i föregående exempel kan skriva om till:
Som ni kan se kan vi alltså uttrycka en hel del av dessa värden med varandra. Om vi nu till exempel kände till stöttalet samt farten så skulle vi kunna räkna ut både och .