Varför ett helt kapitel om detta?
Jo, för att man ofta stöter på väldigt petiga rättare i högre utbildningar. Rättare som anser att en uppgift kan bli totalt underkänd om skissningen av problemet (även kallad friläggningen) har dåligt placerade kraftvektorer. Detta kanske inte verkar så svårt att undvika. För just normalkraften kan det dock vara så att man har kvar en dålig vana från gymnasiet.
Man brukade nämligen placera den antingen lite hur som helst eller i samma led som tyngdkraften. I vissa fall är blir detta tyvärr inte helt verklighetstroget.
Nu när vi lärt oss att krafter ofta orsakar vridningar, måste vi ta hänsyn till normalkraftens placering, då den inte bara måste motverka krafterna som utövas på kontaktytan, utan även deras vridningar.
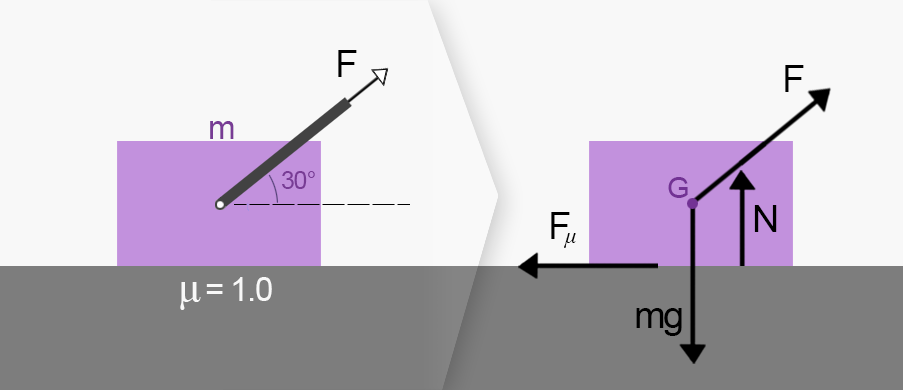
Ta denna låda till exempel. Normalkraften kommer som vi redan vet hindra lådan från att bara åka rakt igenom golvet. Men dess placering är också viktig! Krafterna riskerar nämligen att orsaka vridning på lådan om vi placerar fel.
För att lådan inte ska tippa över, måste krafternas vridningar motverka varandra.
kommer alltid att ligga längs kontaktytan, i detta fall orsakar den en vridning i punkten .
har vi inte heller "friheten" att röra på, i med att den borde utgå ifrån masscentrum. Tyngdkraften orsakar dock ingen vridning i punkten .
Vi har då bara ett val kvar, att placera på en läglig plats.
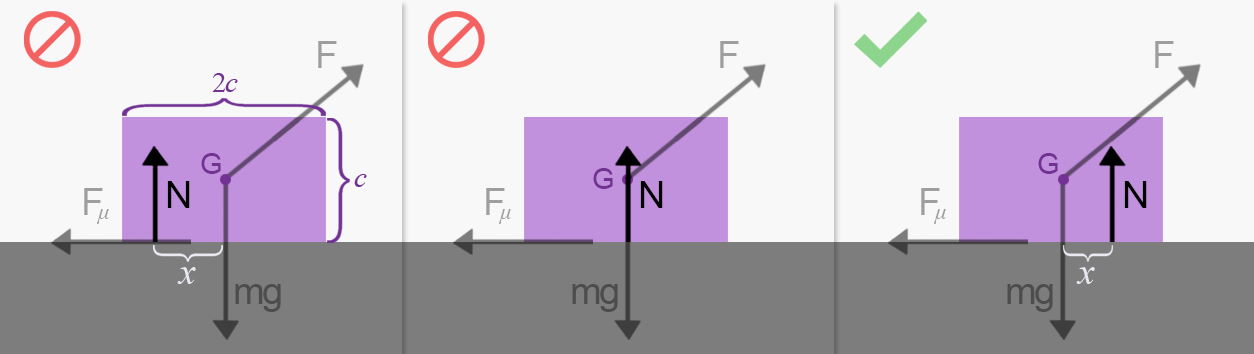
Om vi nu som på gymnasiet placerade längs samma verkningslinje som , så skulle inte orsaka någon vridning, eftersom den då, som skulle ha en verkningslinje som går igenom . Då skulle få lådan att tippa över.
Ok, men hur ska vi placera den då? Låt vara avståndet mellan och :s verkningslinje. Vi ansätter dessutom lådans bredd till och dess höjd till .
Vi får då att
Som ni se har jag satt som tecken för , eftersom normalkraftens vridning i punkten är negativ om är till vänster om och positiv om är till höger.
Vi kan alltså redan nu dra slutsatsen att måste vara till höger om på höger sida om ska bli .
Nu är då frågan om vi borde räkna vidare, för om vi skulle vilja veta var bör placeras exakt, så måste vi ställa upp de resterande jämviktsekvationerna.
Man behöver dock oftast bara tillämpa det här under friläggningen. Därför bör detta tänk ske snabbt i huvet innan man skissar, för att veta var borde sitta. De enda gångerna man förväntas göra dessa beräkningar är då man specifikt ombeds räkna ut Normalkraftens angreppspunkt.