Kurvintegraler & Greens formel

Vad är en kurvintegral?

Vi har först ett vektorfält $F(x,y)$ som kan ritas upp som en yta i x,y,z-planet (vi har markerat ytan med lila färg på bilden nedan).

Vi har sedan en vanlig envariabelsfunktion $c(x)$ som ritar upp en tvådimensionell kurva $C$ i x,y-planet (den oranga kurvan längst ner på bilden).

Tänk er nu alla punkter mellan vår tredimensionella yta och kurvan $C$. Dessa bildar en slags "sned vägg": på bilden nedan är detta den blåa ytan $D$.

Det är den ytan som vi är intresserade av.

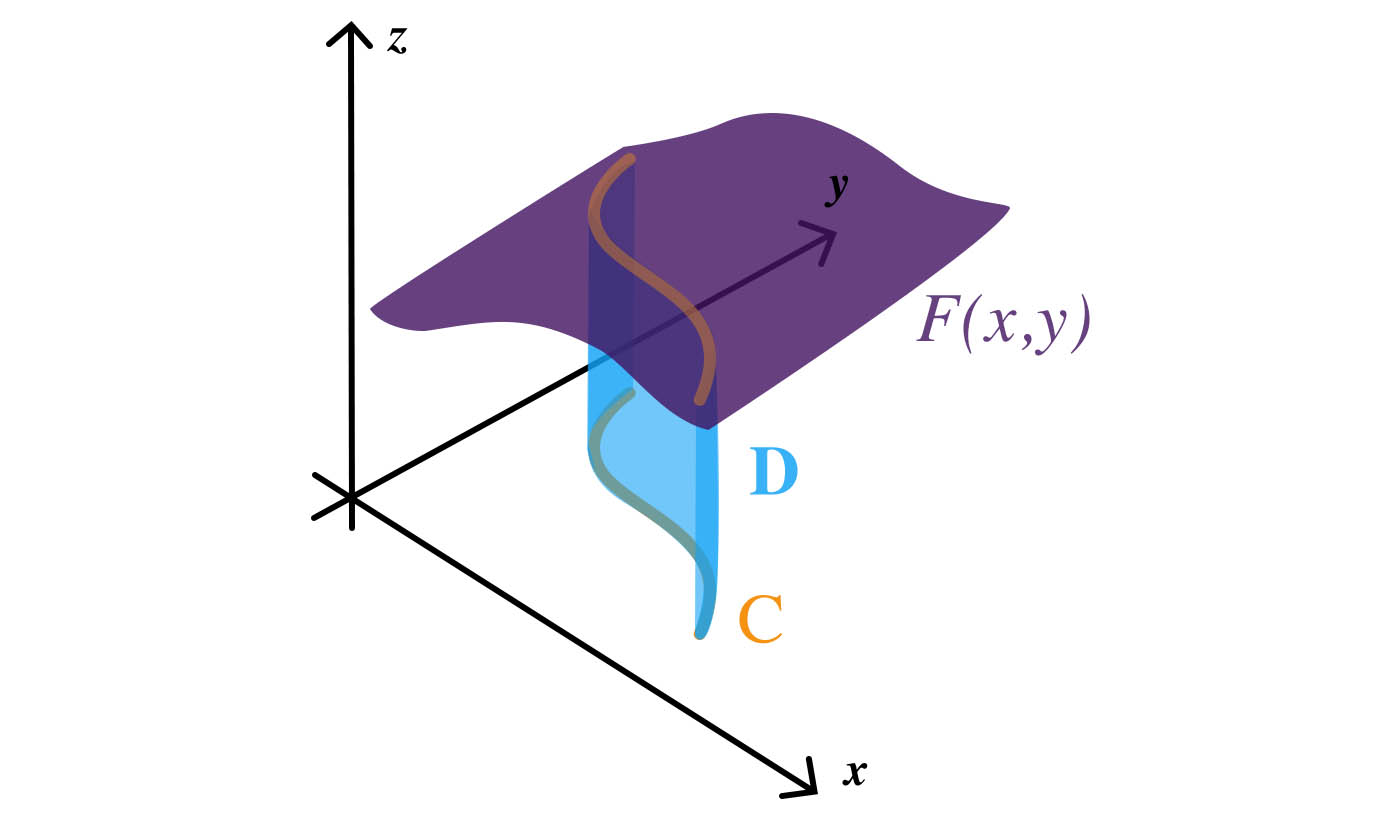
Det finns ett annat (mer matematiskt) sätt att förklara vad arean på ytan $D$ är, nämligen kurvintegralen av $F(x,y)$ längs $C$. Denna kurvintegral betecknas såhär: $\int _{ C }^{ }{ F(x,y)ds }$

Räkna ut kurvintegralen

Om vi har ett vektorfält $F$ och en parametriserad kurva $C$ (alltså en kurva som vi känner till värdemängden på), sådan att $C=r(t)=(x(t),y(t))$, $a\le t\le b$, så kan vi räkna ut kurvintegralen av $F$ längs $C$ med följande formel:

Exempel:

Låt $\vec { F } =(2y,2x,z+y)$. Beräkna kurvintegralen av $\vec { F }$ längs sträckan $AB$ då $A=(1,1,1)$ och $B=(2,2,3)$.

Lösning:

Här har vi ett enkelt exempel då sträckan $AB$ är en rät linje. Vi börjar med att räkna ut den här linjens ekvation. Vi tar först fram dess riktningsvektor: $B-A=(2,2,3)-(1,1,1)=(1,1,2)$.

Riktningsvektorn är alltså $(1,1,2)t$.

Vi väljer nu $A$ som startpunkt och får att linjens ekvation är: $r(t)=(1+t,1+t,1+2t)$.

Eftersom linjen ska vara parametriserad måste vi hitta värdena $a$ och $b$ (från definitionen ovan), som insatta i $r(t)$ ger linjens värdemängd.

Vi vet att i det här fallet är linjens största värde $B=(2,2,3)$ och dess minsta är $A=(1,1,1)$. För att $r(t)=A$ måste vi ha $t=0$. För att $r(t)=B$ måste vi ha $t=1$.

Alltså får vi: $0\le t\le 1$.

Vi ska nu applicera formeln från definitionen! För att integreringen ska ske så enkelt som möjligt kan vi första räkna ut allts som finns inuti den. Vi sätter först in $r(t)$ i $F$:

$\vec { F } (r(t))=(2(1+t),2(1+t),(1+2t)+(1+t))=(2+2t,2+2t,2+3t)$.

Vi räknar också ut derivatan till $r$: $r'(t)=(1,1,2)$.

Slutligen räknar vi ut $\vec { F } (r(t))\bullet r'(t)$:

$\vec { F } (r(t))\bullet r'(t)=(1(2+2t))+(1(2+2t))+(2(2+3t))$

$=2+2t+2+2t+4+6t$

$=10t+8$

Nu är det äntligen bara att använda formeln och sätta in allt som vi har räknat ut:

$\int _{ AB }^{ }{ F\bullet dr } =\int _{ a }^{ b }{ F(r(t)) } \bullet r'(t)dt$

$=\int _{ 0 }^{ 1 }{ 10t+8 } dt$

$={ \left[ 5{ t }^{ 2 }+8t \right] }_{ 0 }^{ 1 }$

$=5+8$

$=13$

Greens formel

Om $C$ är en sluten kurva (d.v.s. att den har samma start- och ändpunk) som omsluter området $D$, och $\vec { F } (P,Q)$ är ett vektorfält, kan vi beräkna kurvintegralen av $F$ längs $C$ med Greens formel:

Exempel:

Låt $\vec { F } =({ e }^{ { x }^{ 2 } }+{ x }^{ 2 }y,{ y }^{ 2 }+sin(y))$. Beräkna kurvintegralen $\int _{ C }^{ }{ F\bullet dr }$ längs cirkeln ${ x }^{ 2 }+{ y }^{ 2 }=1$, genomlöpt ett varv i positiv riktning (moturs).

Lösning:

Eftersom kurvan $C$ är en cirkel vet vi att den också är sluten! Vi kan alltså använda Greens formel! Vi räknar först ur de partiella derivatorna till $F$:

• $\frac { \partial Q }{ \partial x } =0$

• $\frac { \partial P }{ \partial y } ={ x }^{ 2 }$

Vi skriver nu upp Greens formel och sätter in våra partiella derivator:$\int _{ C }^{ }{ F\bullet dr } =\iint _{ D }^{ }{ (\frac { \partial Q }{ \partial x } -\frac { \partial P }{ \partial y } ) } dxdy=\iint _{ D }^{ }{ (-{ x }^{ 2 }) } dxdy$

Eftersom vi integrerar på en cirkel måste vi omvandla allt till polära koordinater innan vi integrerar. Vi får då:

• $-{ x }^{ 2 }=-{ r }^{ 2 }{ cos }^{ 2 }\varphi$

• $dxdy=rdrd\varphi$

Vi vet också att vår första integration ska gå från $0$ till $1$ (eftersom cirkeln har radien 1), och att den andra ska gå från $0$ till $2\pi$ (eftersom vi genomlöper cirkeln ett varv i positiv riktning).

Vi ersätter våra värden i Greens formel med alla dessa och får då:

$\int _{ 0 }^{ 2\pi }{ \int _{ 0 }^{ 1 }{ (-{ r }^{ 2 }{ cos }^{ 2 }\varphi ) } rdrd\varphi }$

$=\int _{ 0 }^{ 2\pi }{ { (cos }^{ 2 }\varphi )d\varphi \int _{ 0 }^{ 1 }{ (-{ r }^{ 2 }) } rdr }$

$=\int _{ 0 }^{ 2\pi }{ { (cos }^{ 2 }\varphi )d\varphi \int _{ 0 }^{ 1 }{ (-{ r }^{ 3 }) } dr }$

Vi har nu två integraler som vi måste räkna ut. Vi börjar med den första (som är svårast)!

$\int _{ 0 }^{ 2\pi }{ { (cos }^{ 2 }\varphi )d\varphi }$

Som ni kanske kommer ihåg från envariabelanalysen kan man ersätta ${ \cos }^{ 2 }\varphi$ med $\frac { 1+{ \cos }(2\varphi ) }{ 2 }$:

$=\int _{ 0 }^{ 2\pi }{ (\frac { 1+cos(2\varphi ) }{ 2 } )d\varphi }$

$=\frac { 1 }{ 2 } \int _{ 0 }^{ 2\pi }{ (1+cos(2\varphi ))d\varphi }$

Vi gör substitutionen $t=2\varphi$ , detta ger att:

$t=2\varphi \Rightarrow \frac { dt }{ d\varphi } =\frac { d }{ d\varphi } \left( 2\varphi \right) \Rightarrow \frac { dt }{ d\varphi } =2\Rightarrow dt=2d\varphi$ med de nya integrationsgränserna $\varphi =0\Rightarrow t=0,\quad \varphi =2\pi \Rightarrow t=4\pi$

Vi utför substitutionen i vår integral:

$=\frac { 1 }{ 2 } \int _{ 0 }^{ 4\pi }{ (1+cos(t))\frac { 1 }{ 2 } dt }$

$=\frac { 1 }{ 4 } \int _{ 0 }^{ 4\pi }{ (1+cos(t))dt }$

$=\frac { 1 }{ 4 } { \left[ t+sin(t) \right] }_{ 0 }^{ 4\pi }dt$

$=\frac { 1 }{ 4 } ((4\pi +sin(4\pi ))-(0+sin(0)))$

$= \pi$

Phew, det ver en jobbig integral! Men nu kan vi i alla fall gå tillbaka till Greens formel och ersätta den första integralen med $$\pi$$

$=\int _{ 0 }^{ 2\pi }{ { (cos }^{ 2 }\varphi )d\varphi \int _{ 0 }^{ 1 }{ (-{ r }^{ 3 }) } dr }$

$=\pi \int _{ 0 }^{ 1 }{ (-{ r }^{ 3 }) }$

...och som tur är så är den andra integralen mycket enklare att beräkna så nu är det bara att fortsätta!

$=\pi { \left[ \frac { { -r }^{ 4 } }{ 4 } \right] }_{ 0 }^{ 1 }$ $=\frac { -\pi }{ 4 }$

Nu är vi äntligen klara! Kurvintegralen till F längs cirkeln genomlöpt ett varv i positiv riktning är alltså $\frac { -\pi }{ 4 }$

Konservativa vektorfält

Om $\vec { F }$ är ett konservativt vektorfält, finns det en ännu enklare formel för att räkna ut kurvintegralen av $\vec { F }$längs en kurva C som går från $A$ till $B$:

$\int _{ C }^{ }{ F\bullet dr } =U(B)-U(A)$

Tips! När ni ska räkna ut kurvintegralen till ett vektorfält, kolla alltid först om fältet är konservativt! Om det är det kan ni använda den här formeln, vilket vanligtvis sparar mycket tid!

Exempel:

Vi har ett vektorfält $\vec { F } =(2x,cos(y))$. Beräkna en kurvintegral till vektorfältet som går från punkten $A(0,0)$ till $B(1,\frac { \pi }{ 2 } )$.

Lösning:

Vi ser att funktionerna $g(x,y)=2x$ och $h(x,y)=cos(y)$ är kontinuerliga. För att kontrollera att F är konservativt ska vi alltså räkna ut derivatan till 2x med avseende på y, och derivatan till cos(y) med avseende på x och se om de är lika.

Vi får att: $\frac { \partial g }{ \partial y } =\frac { \partial h }{ \partial x } =0$, alltså är fältet konservativt!

Vi kan nu använda den enkla formeln:

$\int _{ C }^{ }{ F\bullet dr } =U(B)-U(A)$

Vi måste bara räkna ut funktionen $U(x,y)$ (potentialen) först!

Vi ställer upp ekvationssystemet:

• ${ U' }_{ x }=2x$

• ${ U' }_{ y }=cos(y)$

Den första ekvationen ger att $U={ x }^{ 2 }+f(y)$.

Vi sätter nu ${ f' }(y)=cos(y)$ (andra ekvationen), och får då $f(y)=sin(y)$.

Nu har vi hittat potentialen vi sökte! $U={ x }^{ 2 }+sin(y)$.

Nu återstår det bara att använda formeln och sätta in punkterna $A$ och $B$ :

$\int _{ C }^{ }{ F\bullet dr } =U(B)-U(A)$

$=(2)-0^{ 2 }+sin(0)$

$=2$

Kurvintegralen är alltså lika med 2!