Vad är en serie?
En serie är en summering av ett oändligt antal termer.
Vi kan till exempel tänka oss serien som fortsätter i all oändlighet! Denna kan också skrivas som .
Den här notationen betyder att man börjar på , och sedan summerar alla -termer ända fram till "slutstationen" (som i det här fallet är och som aldrig kommer uppnås).
Konvergens och divergens
Om termerna i en serie minskar tillräckligt fort kan summan gå mot ett ändligt tal, man säger då att serien konvergerar.
Ett annat (lite mer matematiskt) sätt att formulera detta på är att serien är konvergent om gränsvärdet existerar. Om gränsvärdet inte existerar säger man istället att serien är divergent (serien går mot oändligheten).
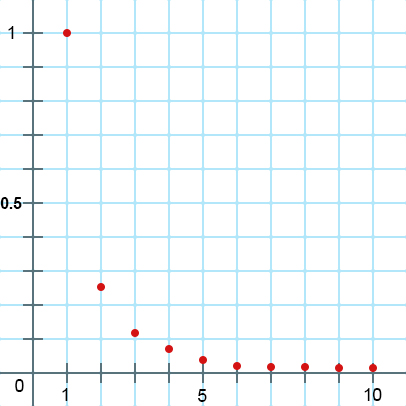
Ett exempel på en konvergerande serie är som ger
På bilden nedan ser vi tydligt att termerna går mot ju längre serien blir.
⚠️ OBS!
Till skillnad från vad man intuitivt kan tro så är serien inte konvergent, utan divergent. Anledningen till detta är att termerna inte blir tillräckligt små tillräckligt snabbt helt enkelt.
kallas därför också för den harmoniska serien.
Uträkning
På tentor måste man ofta ta reda på om en serie är konvergent eller divergent. Det finns flera sätt att göra detta på, i de flesta fall handlar det om att skriva om en svår serie till något enklare som man redan känner till.
P-testet
konvergerar om och divergerar om
Geometriska serier konvergerar om är mellan och
Divergenstestet
Om vi har en serie där inte är lika med , så är serien divergent.
Om är serien obestämd.Det här borde vara det första testet du utför när du får en serie, eftersom du kan spara mycket tid om det direkt visar sig att serien divergerar!
Jämförelsetestet
Om vi har 2 serier och som bara innehåller positiva termer, och där för alla , så har vi:
Om (den större serien) konvergerar så konvergerar också
Om (den mindre serien) divergerar så divergerar också
Gränsvärdetestet
Vi har 2 serier och som liknar varandra och som bara innehåller positiva termer.
Om gränsvärdet ger ett ändligt tal som inte är lika med , så uppför sig serierna på samma sätt (antingen är båda divergenta, eller så är båda konvergenta).
Absolut konvergens
Om konvergerar så gör även det!
Uppgift 1
Undersök om serien är konvergent eller divergent.
Lösning
Vi skriver om serien till en geometrisk serie!
Vi får
Vi har nu serien under formen (konstanten 9 spelar ingen roll), där
Eftersom är mellan och vet vi alltså att serien konvergerar!
Uppgift 2
Undersök om serien är konvergent eller divergent.
Lösning
Eftersom vi vet att cosinustermen aldrig blir särskilt stor kan vi anta att seriens termer uppför sig på samma sätt som , vilket i sin tur är detsamma som (vi delar bara nämnaren och täljaren med ), som är en serie vi känner till!
Vi har alltså 2 serier som liknar varandra: och den harmoniska serien .
Skulle vi kunna använda jämförelsetestet?
Vi ser att båda serierna bara kan innehålla positiva termer, eftersom vi börjar på och eftersom vilket gör att
Slutligen vet vi att alltid kommer att vara större än eftersom vi subtraherar ett positivt tal från nämnaren (och ju mindre nämnaren är, desto större blir termen).
Serierna uppfyller alltså alla krav för jämförelsetestet, och eftersom vi vet att (den mindre serien) divergerar, så divergerar även (den större serien)!