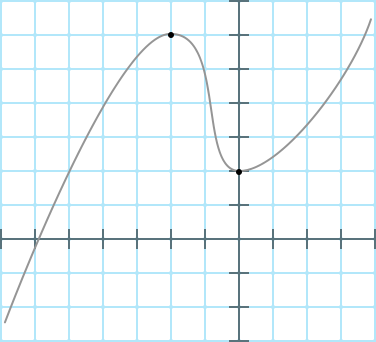
Derivator är väldigt användbara för att hitta hur kurvan till en funktion ser ut.
Om derivatan till en funktion är negativ är funktionens kurva avtagande
Om derivatan till en funktion är positiv är funktionens kurva växande
Det bästa sättet att förstå detta är att gå igenom ett exempel.
Ett enkelt exempel
Låt säga att vi vill hitta hur kurvan till funktionen ser ut.
Vi börjar med att derivera funktionen för att hitta funktionens stationära punkter:
Här ser vi att derivatan blir noll när eller när . Det är alltså vid de här punkterna som funktionen svänger.
Vi ritar nu upp en tabell på följande sätt:
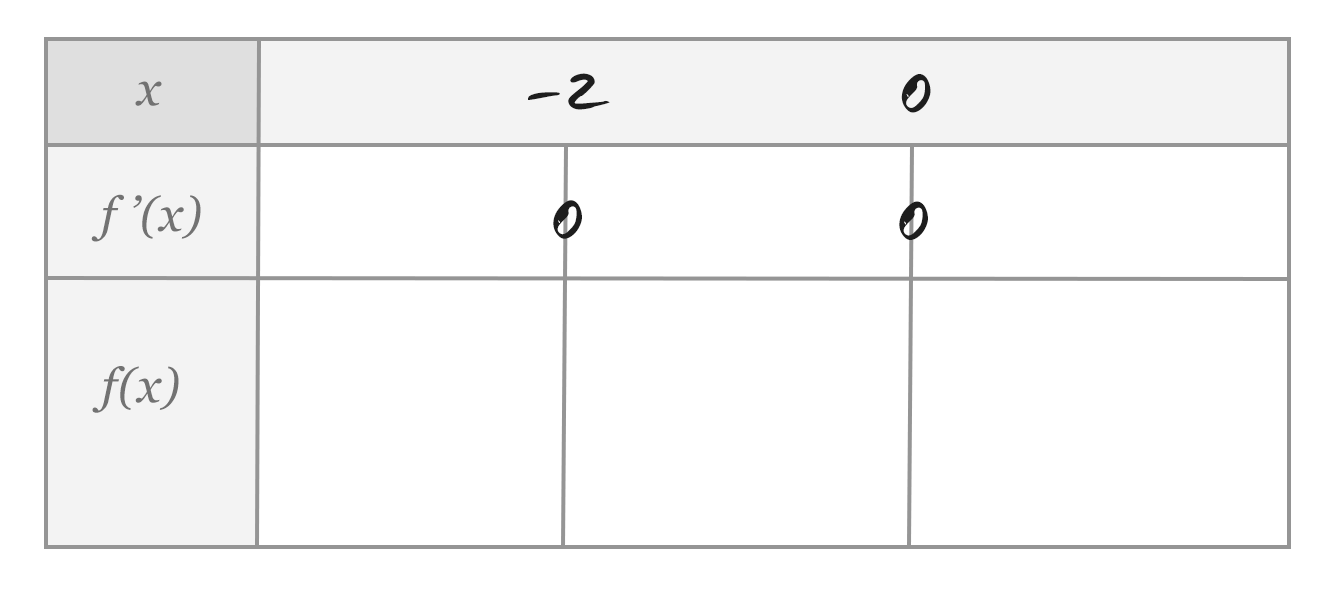
Vi behöver nu fylla i det som saknas. För att göra det behöver vi:
Ett tal som är mindre än
Ett tal som är större än men mindre än
Ett sista tal som är större än
Vi väljer till exempel , och . Vi sätter in de här talen i deriveringsfunktionen för att se om resultatet blir positivt eller negativt.
, som är positivt
, som är negativt
, som är positivt
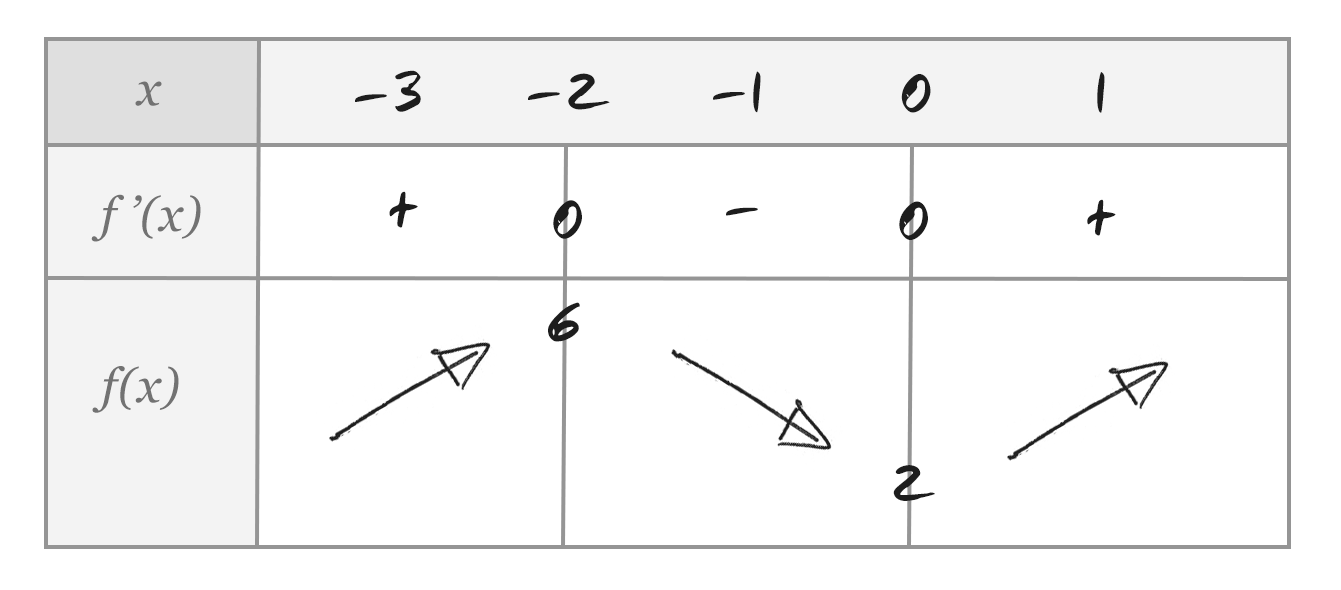
Vi vet alltså nu var derivatan är positiv och negativ, och därför också var funktionen är växande och var den är avtagande!
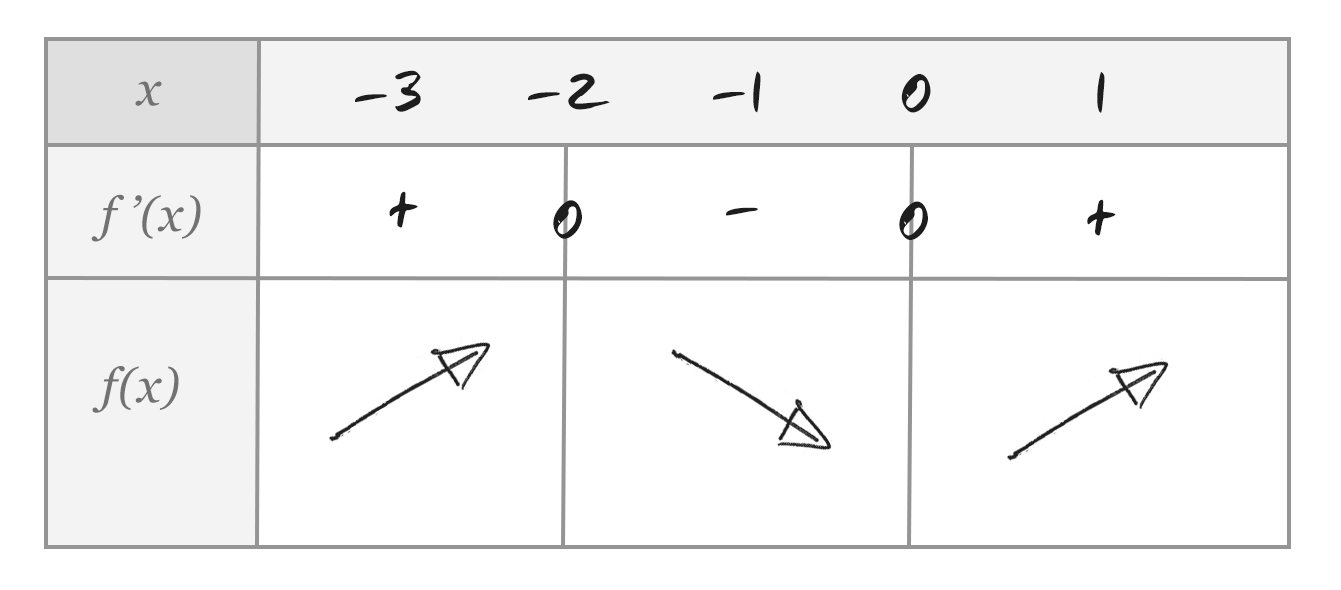
Vi vet nu att funktionen har en maxpunkt vid och en minimipunkt vid . Vi kan nu räkna ut vilket värde funktionen antar vid dessa punkter: