Alla funktioner har en viss definitionsmängd och en värdemängd. Ett sätt att förklara det på är att tänka oss en funktion .
Ersätt med . Funktionen ska alltså nu vara skriven som: termer som innehåller
Trixa lite med ekvationen till du har isolerat och får fram: termer som innehåller
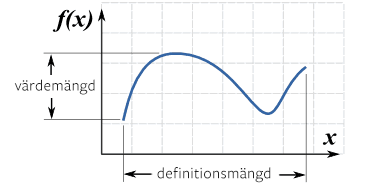
Definitionsmängd
Definitionsmängden till en funktion betecknas . Vilka -värden som är tillåtna varierar från funktion till funktion.
Ett enkelt exempel är funktionen . Här får absolut inte vara (eftersom det inte går att dela något med noll)!
Definitionsmängden till är alltså i det här fallet: .
Värdemängd
Värdemängden till en funktion betecknas . Man kan få fram den på olika sätt efter att ha hittat definitionsmängden, t.ex. genom att räkna ut funktionens gränsvärden, rita upp en teckentabell, eller bara genom att tänka till lite.
Ett enkelt exempel är funktionen . Denna har alla reella tal () som definitionsmängd, men kan aldrig anta ett negativt värde, oavsett vad är.
Värdemängden till funktionen är alltså i det här fallet (d.v.s. alla positiva reella tal).
Invers funktion
En invers funktion betecknas och innebär att variabelns och funktionens värde byter plats med varandra. Detta medför också att:
Definitionsmängden till blir värdemängden till
Värdemängden till blir definitionsmängden till
Kort sagt byter alltså definitionsmängden och värdemängden plats när man tar fram inversen till en funktion.
Hur får man då fram en invers funktion? Låt säga att vi har en funktion . Vi följer nu dessa steg för att få fram dess invers:
Ersätt med . Funktionen ska alltså nu vara skriven som: termer som innehåller
Trixa lite med ekvationen till du har isolerat och får fram: termer som innehåller
Ersätt med och med ! Grattis, du har nu fått fram funktionens invers!
För att kontrollera att du har förstått allting i det här kapitlet kan du göra nedanstående uppgift. Försök först att lösa den själv och kolla sedan på lösningen!
Uppgift
Vi har funktionen
Beräkna funktionens invers
Hitta inversens värdemängd
Hitta inversens definitionsmängd
Lösning
Vi börjar med att hitta funktionens invers! Vi kommer att gå igenom varje steg i detalj, så var inte orolig om det ser långt ut.
Vi ersätter först "" med :
Nu ska vi isolera :
Slutligen ersätter vi med och med :
Nu har vi vår inversfunktion! Nästa steg är att hitta värdemängden till inversen!
Som vi såg förut är inversfunktionens värdemängd densamma som funktionens definitionsmängd.
Vi kan enkelt se att definitionsmängden till är , alltså har vi även:
Slutligen ska vi hitta inversens definitionsmängd, d.v.s. originalfunktionens värdemängd.
För att hitta definitionsmängden till inversen kan vi se när funktionen blir ogiltig genom använda en slags "uteslutningsmetod" och se när dess olika termer är odefinierade.
Vi vet först och främst att endast är definierad när , alltså är mängden redan utesluten.
Vi vet också att nämnaren i ett bråk aldrig får anta . I det här fallet är nämnaren , och antar alltså när . Alltså är även utesluten ur definitionsmängden.
Utifrån dessa två definitionsmängder vet vi nu att inversens definitionsmängd är .